1567. Сумма и произведение
Список
неотрицательных чисел называется удовлетворительным, если их сумма равна s, а произведение p. Найти удовлетворительный список с наименьшим количеством
элементов.
Вход. Каждая строка является отдельным тестом и содержит два
неотрицательных целых числа s и p (1 ≤ s, p ≤ 109).
Выход. Для каждого теста в отдельной строке вывести наименьший
возможный размер удовлетворительного списка. Если искомого списка не
существует, то вывести -1. Отметим, что список содержит не обязательно целые
числа.
|
Пример
входа |
Пример
выхода |
|
10 10 5 6 5 100 |
1 2 -1 |
РЕШЕНИЕ
математика
Анализ алгоритма
В задаче следует
найти наименьшее n, для которого
существуют такие x1, x2, …, xn, что
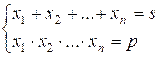
Рассмотрим, какие значения может принимать произведение x1 * x2 * … * xn
для заданных n и s. Если n = 1, то
решением будет x1 = s = p.
При n = 2 сумма x1 + x2
= s, произведение равно x1 * x2 = x1
* (s – x1). Рассмотрим, какие значения может принимать
произведение. Решим уравнение x * (s – x)
= p или x2 – s * x + p
= 0. Дискриминант уравнения равен D = s2
– 4 * p. Уравнение имеет решение при
D ³ 0 или p £ s2 / 4
. Если p ³ 0, то решения
x1,2 =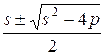 
будут неотрицательными. Таким образом, с помощью двух
действительных чисел, сумма которых равна s, можно получить любое произведение
от 0 до s2 / 4. При этом
наибольше произведение s2
/ 4 можно получить при x1
= x2 = s / 2.
Лемма. Если сумма n
чисел равна s, то их максимально
произведение равно (s / n)n
и достигается при x1 = x2 = … = xn = s / n.
Если
предположить противное, то найдется наименьшее m = xi и
наибольшее M = xj среди этих чисел. Заменим m и M на числа (m + M)
/ 2 и (m + M) / 2. В таком случае произведение x1 * x2
* … * xn увеличится.
Доказательство. Докажем неравенство 
. Имеем: 
, 
, что верно так как по предположению m и M не равны между
собой.
Теорема. Если сумма n чисел равна s, то их
произведение может принимать любое значение от 0 до (s / n)n.
Согласно лемме,
наибольшее значение (s / n)n
достигается при x1 = x2 = … = xn = s / n. Осталось показать, что достигается и
любое другое произведение p, 0 £ p £ (s / n)n. Доказательство проведем
конструктивно.
Возьмем b = p
/ (s / n)n-2.
Очевидно, что 0 £ b £ (s / n)2. Исходя из выше
доказанного, существуют такие x1
и x2, что x1 + x2 = 2 * s / n, x1
* x2 = b £ (2 * s / n)2 / 4 = (s / n)2.
Добавим значения x3 = x4 = … = xn = s / n чтобы получить требуемые n чисел: x1 + x2
+ … + xn = 2 * s / n
+ (n – 2) * s / n = s, x1
* x2 * … * xn = b * (s / n)n-2
= p.
Таким образом, алгоритм
решения задачи состоит в следующем:
1. Если s = p,
то вернуть 1.
2.
Последовательно перебираем n = 2, 3,
…, s. Как только станет p £ (s / n)n, возвращаем n.
3. Если на втором
шаге решение не найдено, то возвращаем -1.
Пример. Найти n = 5 чисел, сумма которых равна s = 10, а произведение p
= 30.
Такие числа
существуют, так как p ≤ (s / n)n = (10 / 5)5 =
32. Выберем такие x1 и x2, что x1 + x2
= 2 * s / n = 2 * 10 / 5 = 4, а их произведение равно b = p / (s / n)n-2 = 30 / (10 /
5)3 = 30 / 8 = 15 / 4. Такие числа существуют согласно лемме.
Выберем x3 = x4 = x5 = s / n = 10 / 5 = 2. Указанные пять чисел и
будут являться ответом.
Реализация алгоритма
Функция smallestSet по
заданным s и p возвращает искомое наименьшее значение n.
int smallestSet(int
s, int p)
{
int n;
if (s == p) return 1;
for(n = 2; n
<= s; n++)
if (pow(1.0
* s / n, 1.0 * n) >= p) return n;
return -1;
}
Основная часть программы.
while(scanf("%d %d",&s, &p) == 2)
{
res = smallestSet(s,p);
printf("%d\n",res);
}